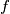
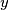
Let be any function that maps the set of real numbers into the set of real numbers. Prove that there exist real numbers and such that
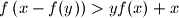
Proposed by Igor Voronovich, Belarus
%V0
Let $f$ be any function that maps the set of real numbers into the set of real numbers. Prove that there exist real numbers $x$ and $y$ such that $$f\left(x-f(y)\right)>yf(x)+x$$
Proposed by Igor Voronovich, Belarus
Izvor: Međunarodna matematička olimpijada, shortlist 2009
Školjka 
be any function that maps the set of real numbers into the set of real numbers. Prove that there exist real numbers 
and 
such that 