IMO Shortlist 2009 problem C2
Dodao/la:
arhiva2. travnja 2012. For any integer
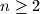
, let
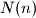
be the maxima number of triples
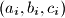
,

, consisting of nonnegative integers
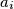
,
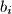
and
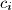
such that the following two conditions are satisfied:
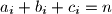
for all

, If
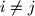
then
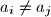
,
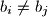
and
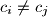
Determine
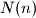
for all
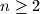
.
Proposed by Dan Schwarz, Romania
%V0
For any integer $n\geq 2$, let $N(n)$ be the maxima number of triples $(a_i, b_i, c_i)$, $i=1, \ldots, N(n)$, consisting of nonnegative integers $a_i$, $b_i$ and $c_i$ such that the following two conditions are satisfied:
$a_i+b_i+c_i=n$ for all $i=1, \ldots, N(n)$, If $i\neq j$ then $a_i\neq a_j$, $b_i\neq b_j$ and $c_i\neq c_j$Determine $N(n)$ for all $n\geq 2$.
Proposed by Dan Schwarz, Romania
Izvor: Međunarodna matematička olimpijada, shortlist 2009