Let

be a positive integer. Given a sequence
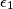
, ...,
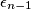
with
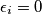
or
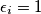
for each
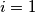
, ...,
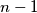
, the sequences
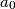
, ...,

and
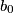
, ...,
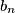
are constructed by the following rules:
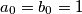
,
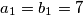
,
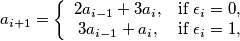
for each
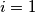
, ...,
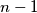
,
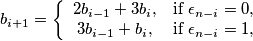
for each
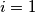
, ...,
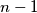
.
Prove that
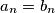
.
Proposed by Ilya Bogdanov, Russia
%V0
Let $n$ be a positive integer. Given a sequence $\epsilon_1$, ..., $\epsilon_{n - 1}$ with $\epsilon_i = 0$ or $\epsilon_i = 1$ for each $i = 1$, ..., $n - 1$, the sequences $a_0$, ..., $a_n$ and $b_0$, ..., $b_n$ are constructed by the following rules: $a_0 = b_0 = 1$, $a_1 = b_1 = 7$,
$$a_{i + 1} = \left\{\begin{array}{cl}2a_{i - 1} + 3a_i\text{,} & \text{if } \epsilon_i = 0 \text{,}\\3a_{i - 1} + a_i\text{,} & \text{if } \epsilon_{i}= 1,\end{array}\right.$$
for each $i = 1$, ..., $n - 1$,
$$b_{i + 1} = \left\{\begin{array}{cl}2b_{i - 1} + 3b_i\text{,} & \text{if } \epsilon_{n - i} = 0 \text{,}\\3b_{i - 1} + b_i\text{,} & \text{if } \epsilon_{n - i} = 1 \text{,}\end{array}\right.$$
for each $i = 1$, ..., $n - 1$.
Prove that $a_n = b_n$.
Proposed by Ilya Bogdanov, Russia