IMO Shortlist 2009 problem C4
Kvaliteta:
Avg: 0,0Težina:
Avg: 7,0 For an integer 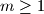 , we consider partitions of a
, we consider partitions of a 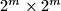 chessboard into rectangles consisting of cells of chessboard, in which each of the
chessboard into rectangles consisting of cells of chessboard, in which each of the 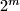 cells along one diagonal forms a separate rectangle of side length
cells along one diagonal forms a separate rectangle of side length 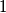 . Determine the smallest possible sum of rectangle perimeters in such a partition.
. Determine the smallest possible sum of rectangle perimeters in such a partition.
Proposed by Gerhard Woeginger, Netherlands
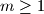 , we consider partitions of a
, we consider partitions of a 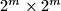 chessboard into rectangles consisting of cells of chessboard, in which each of the
chessboard into rectangles consisting of cells of chessboard, in which each of the 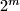 cells along one diagonal forms a separate rectangle of side length
cells along one diagonal forms a separate rectangle of side length 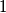 . Determine the smallest possible sum of rectangle perimeters in such a partition.
. Determine the smallest possible sum of rectangle perimeters in such a partition.Proposed by Gerhard Woeginger, Netherlands
Izvor: Međunarodna matematička olimpijada, shortlist 2009
 Školjka
Školjka 
