IMO Shortlist 2009 problem G3
Dodao/la:
arhiva2. travnja 2012. Let

be a triangle. The incircle of

touches the sides

and

at the points

and

, respectively. Let

be the point where the lines
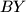
and
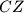
meet, and let

and

be points such that the two quadrilaterals
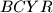
and
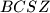
are parallelogram.
Prove that
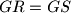
.
Proposed by Hossein Karke Abadi, Iran
%V0
Let $ABC$ be a triangle. The incircle of $ABC$ touches the sides $AB$ and $AC$ at the points $Z$ and $Y$, respectively. Let $G$ be the point where the lines $BY$ and $CZ$ meet, and let $R$ and $S$ be points such that the two quadrilaterals $BCYR$ and $BCSZ$ are parallelogram.
Prove that $GR=GS$.
Proposed by Hossein Karke Abadi, Iran
Izvor: Međunarodna matematička olimpijada, shortlist 2009