IMO Shortlist 2009 problem G7
Dodao/la:
arhiva2. travnja 2012. Let

be a triangle with incenter

and let

,
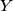
and
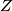
be the incenters of the triangles
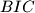
,
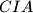
and
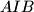
, respectively. Let the triangle
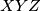
be equilateral. Prove that

is equilateral too.
Proposed by Mirsaleh Bahavarnia, Iran
%V0
Let $ABC$ be a triangle with incenter $I$ and let $X$, $Y$ and $Z$ be the incenters of the triangles $BIC$, $CIA$ and $AIB$, respectively. Let the triangle $XYZ$ be equilateral. Prove that $ABC$ is equilateral too.
Proposed by Mirsaleh Bahavarnia, Iran
Izvor: Međunarodna matematička olimpijada, shortlist 2009