IMO Shortlist 2009 problem N4
Dodao/la:
arhiva2. travnja 2012. Find all positive integers

such that there exists a sequence of positive integers

,

, ...,

satisfying
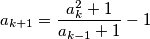
for every

with
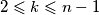
.
Proposed by North Korea
%V0
Find all positive integers $n$ such that there exists a sequence of positive integers $a_1$, $a_2$, ..., $a_n$ satisfying
$$a_{k+1}=\frac{a_k^2+1}{a_{k-1}+1}-1$$ for every $k$ with $2 \leqslant k \leqslant n-1$.
Proposed by North Korea
Izvor: Međunarodna matematička olimpijada, shortlist 2009