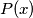
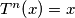
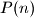
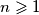
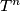
Let be a non-constant polynomial with integer coefficients. Prove that there is no function from the set of integers into the set of integers such that the number of integers with is equal to for every , where denotes the -fold application of .
Proposed by Jozsef Pelikan, Hungary
%V0
Let $P\!\left(x\right)$ be a non-constant polynomial with integer coefficients. Prove that there is no function $T$ from the set of integers into the set of integers such that the number of integers $x$ with $T^n\!\left(x\right) = x$ is equal to $P\!\left(n\right)$ for every $n \geqslant 1$, where $T^n$ denotes the $n$-fold application of $T$.
Proposed by Jozsef Pelikan, Hungary
Izvor: Međunarodna matematička olimpijada, shortlist 2009
Školjka 
be a non-constant polynomial with integer coefficients. Prove that there is no function 
from the set of integers into the set of integers such that the number of integers 
with 
is equal to 
for every 
, where 
denotes the 
-fold application of