IMO Shortlist 2009 problem N6
Dodao/la:
arhiva2. travnja 2012. Let

be a positive integer. Show that if there exists a sequence
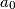
,

, ... of integers satisfying the condition
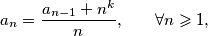
then
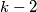
is divisible by

.
Proposed by Turkey
%V0
Let $k$ be a positive integer. Show that if there exists a sequence $a_0$, $a_1$, ... of integers satisfying the condition $$a_n=\frac{a_{n-1}+n^k}{n} \text{,} \qquad \forall n \geqslant 1 \text{,}$$ then $k-2$ is divisible by $3$.
Proposed by Turkey
Izvor: Međunarodna matematička olimpijada, shortlist 2009