IMO Shortlist 2010 problem A4
Dodao/la:
arhiva23. lipnja 2013. A sequence
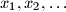
is defined by
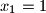
and
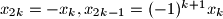
for all
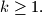
Prove that
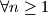
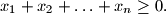
Proposed by Gerhard Wöginger, Austria
%V0
A sequence $x_1, x_2, \ldots$ is defined by $x_1 = 1$ and $x_{2k}=-x_k, x_{2k-1} = (-1)^{k+1}x_k$ for all $k \geq 1.$ Prove that $\forall n \geq 1$ $x_1 + x_2 + \ldots + x_n \geq 0.$
Proposed by Gerhard Wöginger, Austria
Izvor: Međunarodna matematička olimpijada, shortlist 2010