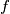
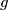
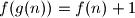
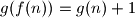
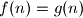
Suppose that and are two functions defined on the set of positive integers and taking positive integer values. Suppose also that the equations and hold for all positive integers. Prove that for all positive integer
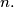
Proposed by Alex Schreiber, Germany
%V0
Suppose that $f$ and $g$ are two functions defined on the set of positive integers and taking positive integer values. Suppose also that the equations $f(g(n)) = f(n) + 1$ and $g(f(n)) = g(n) + 1$ hold for all positive integers. Prove that $f(n) = g(n)$ for all positive integer $n.$
Proposed by Alex Schreiber, Germany
Izvor: Međunarodna matematička olimpijada, shortlist 2010
Školjka 
and 
are two functions defined on the set of positive integers and taking positive integer values. Suppose also that the equations 
and 
hold for all positive integers. Prove that 
for all positive integer 