IMO Shortlist 2010 problem C3
Kvaliteta:
Avg: 3,0Težina:
Avg: 7,0 2500 chess kings have to be placed on a 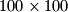 chessboard so that
chessboard so that
(i) no king can capture any other one (i.e. no two kings are placed in two squares sharing a common vertex);
(ii) each row and each column contains exactly 25 kings.
Find the number of such arrangements. (Two arrangements differing by rotation or symmetry are supposed to be different.)
Proposed by Sergei Berlov, Russia
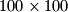 chessboard so that
chessboard so that(i) no king can capture any other one (i.e. no two kings are placed in two squares sharing a common vertex);
(ii) each row and each column contains exactly 25 kings.
Find the number of such arrangements. (Two arrangements differing by rotation or symmetry are supposed to be different.)
Proposed by Sergei Berlov, Russia
Izvor: Međunarodna matematička olimpijada, shortlist 2010
 Školjka
Školjka 
