IMO Shortlist 2010 problem C6
Kvaliteta:
Avg: 0,0Težina:
Avg: 8,0 Given a positive integer  and other two integers
and other two integers 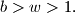 There are two strings of pearls, a string of
There are two strings of pearls, a string of  black pearls and a string of
black pearls and a string of  white pearls. The length of a string is the number of pearls on it. One cuts these strings in some steps by the following rules. In each step:
white pearls. The length of a string is the number of pearls on it. One cuts these strings in some steps by the following rules. In each step:
(i) The strings are ordered by their lengths in a non-increasing order. If there are some strings of equal lengths, then the white ones precede the black ones. Then first ones (if they consist of more than one pearl) are chosen; if there are less than
first ones (if they consist of more than one pearl) are chosen; if there are less than  strings longer than 1, then one chooses all of them.
strings longer than 1, then one chooses all of them.
(ii) Next, one cuts each chosen string into two parts differing in length by at most one. (For instance, if there are strings of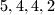 black pearls, strings of
black pearls, strings of 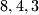 white pearls and
white pearls and 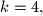 then the strings of 8 white, 5 black, 4 white and 4 black pearls are cut into the parts
then the strings of 8 white, 5 black, 4 white and 4 black pearls are cut into the parts 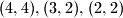 and
and 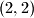 respectively.) The process stops immediately after the step when a first isolated white pearl appears.
respectively.) The process stops immediately after the step when a first isolated white pearl appears.
Prove that at this stage, there will still exist a string of at least two black pearls.
Proposed by Bill Sands, Thao Do, Canada
 and other two integers
and other two integers 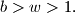 There are two strings of pearls, a string of
There are two strings of pearls, a string of  black pearls and a string of
black pearls and a string of  white pearls. The length of a string is the number of pearls on it. One cuts these strings in some steps by the following rules. In each step:
white pearls. The length of a string is the number of pearls on it. One cuts these strings in some steps by the following rules. In each step:(i) The strings are ordered by their lengths in a non-increasing order. If there are some strings of equal lengths, then the white ones precede the black ones. Then
 first ones (if they consist of more than one pearl) are chosen; if there are less than
first ones (if they consist of more than one pearl) are chosen; if there are less than  strings longer than 1, then one chooses all of them.
strings longer than 1, then one chooses all of them.(ii) Next, one cuts each chosen string into two parts differing in length by at most one. (For instance, if there are strings of
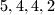 black pearls, strings of
black pearls, strings of 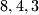 white pearls and
white pearls and 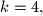 then the strings of 8 white, 5 black, 4 white and 4 black pearls are cut into the parts
then the strings of 8 white, 5 black, 4 white and 4 black pearls are cut into the parts 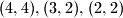 and
and 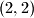 respectively.) The process stops immediately after the step when a first isolated white pearl appears.
respectively.) The process stops immediately after the step when a first isolated white pearl appears.Prove that at this stage, there will still exist a string of at least two black pearls.
Proposed by Bill Sands, Thao Do, Canada
Izvor: Međunarodna matematička olimpijada, shortlist 2010
 Školjka
Školjka 
