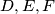
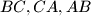
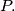
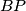
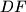
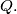
Let be an acute triangle with the feet of the altitudes lying on respectively. One of the intersection points of the line and the circumcircle is The lines and meet at point Prove that
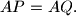
Proposed by Christopher Bradley, United Kingdom
%V0
Let $ABC$ be an acute triangle with $D, E, F$ the feet of the altitudes lying on $BC, CA, AB$ respectively. One of the intersection points of the line $EF$ and the circumcircle is $P.$ The lines $BP$ and $DF$ meet at point $Q.$ Prove that $AP = AQ.$
Proposed by Christopher Bradley, United Kingdom
Izvor: Međunarodna matematička olimpijada, shortlist 2010
Školjka 
be an acute triangle with 
the feet of the altitudes lying on 
respectively. One of the intersection points of the line 
and the circumcircle is 
The lines 
and 
meet at point 
Prove that 