IMO Shortlist 2010 problem G3
Dodao/la:
arhiva23. lipnja 2013. Let
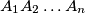
be a convex polygon. Point

inside this polygon is chosen so that its projections
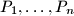
onto lines
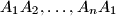
respectively lie on the sides of the polygon. Prove that for arbitrary points
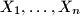
on sides
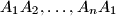
respectively,
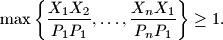
Proposed by Nairi Sedrakyan, Armenia
%V0
Let $A_1A_2 \ldots A_n$ be a convex polygon. Point $P$ inside this polygon is chosen so that its projections $P_1, \ldots , P_n$ onto lines $A_1A_2, \ldots , A_nA_1$ respectively lie on the sides of the polygon. Prove that for arbitrary points $X_1, \ldots , X_n$ on sides $A_1A_2, \ldots , A_nA_1$ respectively,
$$\max \left\{ \frac{X_1X_2}{P_1P_1}, \ldots, \frac{X_nX_1}{P_nP_1} \right\} \geq 1.$$
Proposed by Nairi Sedrakyan, Armenia
Izvor: Međunarodna matematička olimpijada, shortlist 2010