IMO Shortlist 2010 problem G5
Dodao/la:
arhiva23. lipnja 2013. Let
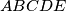
be a convex pentagon such that
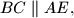
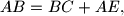
and
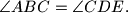
Let

be the midpoint of
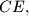
and let

be the circumcenter of triangle
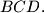
Given that
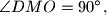
prove that
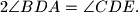
Proposed by Nazar Serdyuk, Ukraine
%V0
Let $ABCDE$ be a convex pentagon such that $BC \parallel AE,$ $AB = BC + AE,$ and $\angle ABC = \angle CDE.$ Let $M$ be the midpoint of $CE,$ and let $O$ be the circumcenter of triangle $BCD.$ Given that $\angle DMO = 90^{\circ},$ prove that $2 \angle BDA = \angle CDE.$
Proposed by Nazar Serdyuk, Ukraine
Izvor: Međunarodna matematička olimpijada, shortlist 2010