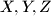
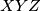
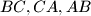
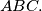
The vertices of an equilateral triangle lie respectively on the sides of an acute-angled triangle Prove that the incenter of triangle lies inside triangle
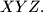
Proposed by Nikolay Beluhov, Bulgaria
%V0
The vertices $X, Y , Z$ of an equilateral triangle $XYZ$ lie respectively on the sides $BC, CA, AB$ of an acute-angled triangle $ABC.$ Prove that the incenter of triangle $ABC$ lies inside triangle $XYZ.$
Proposed by Nikolay Beluhov, Bulgaria
Izvor: Međunarodna matematička olimpijada, shortlist 2010
Školjka 
of an equilateral triangle 
lie respectively on the sides 
of an acute-angled triangle 
Prove that the incenter of triangle 
lies inside triangle 