IMO Shortlist 2010 problem N3
Dodao/la:
arhiva23. lipnja 2013. Find the smallest number

such that there exist polynomials
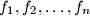
with rational coefficients satisfying
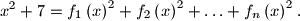
Proposed by Mariusz Skałba, Poland
%V0
Find the smallest number $n$ such that there exist polynomials $f_1, f_2, \ldots , f_n$ with rational coefficients satisfying $$x^2+7 = f_1\left(x\right)^2 + f_2\left(x\right)^2 + \ldots + f_n\left(x\right)^2.$$
Proposed by Mariusz Skałba, Poland
Izvor: Međunarodna matematička olimpijada, shortlist 2010