IMO Shortlist 2010 problem N4
Kvaliteta:
Avg: 0,0Težina:
Avg: 7,0 Let 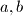 be integers, and let
be integers, and let 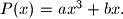 For any positive integer
For any positive integer  we say that the pair
we say that the pair 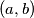 is
is  -good if
-good if 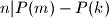 implies
implies 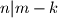 for all integers
for all integers 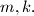 We say that
We say that 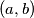 is
is  if
if 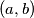 is
is  -good for infinitely many positive integers
-good for infinitely many positive integers 
(a) Find a pair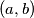 which is 51-good, but not very good.(b) Show that all 2010-good pairs are very good.
which is 51-good, but not very good.(b) Show that all 2010-good pairs are very good.
Proposed by Okan Tekman, Turkey
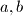 be integers, and let
be integers, and let 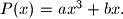 For any positive integer
For any positive integer  we say that the pair
we say that the pair 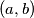 is
is  -good if
-good if 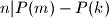 implies
implies 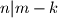 for all integers
for all integers 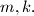 We say that
We say that 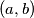 is
is 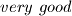 if
if  is
is  -good for infinitely many positive integers
-good for infinitely many positive integers 
(a) Find a pair
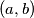 which is 51-good, but not very good.(b) Show that all 2010-good pairs are very good.
which is 51-good, but not very good.(b) Show that all 2010-good pairs are very good.Proposed by Okan Tekman, Turkey
Izvor: Međunarodna matematička olimpijada, shortlist 2010
 Školjka
Školjka 
