IMO Shortlist 2010 problem N6
Kvaliteta:
Avg: 0,0Težina:
Avg: 8,0 The rows and columns of a 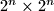 table are numbered from
table are numbered from  to
to 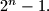 The cells of the table have been coloured with the following property being satisfied: for each
The cells of the table have been coloured with the following property being satisfied: for each 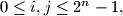 the
the  -th cell in the
-th cell in the  -th row and the
-th row and the 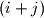 -th cell in the
-th cell in the  -th row have the same colour. (The indices of the cells in a row are considered modulo
-th row have the same colour. (The indices of the cells in a row are considered modulo 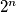 .) Prove that the maximal possible number of colours is
.) Prove that the maximal possible number of colours is 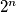 .
.
Proposed by Hossein Dabirian, Sepehr Ghazi-nezami, Iran
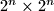 table are numbered from
table are numbered from  to
to 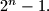 The cells of the table have been coloured with the following property being satisfied: for each
The cells of the table have been coloured with the following property being satisfied: for each 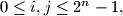 the
the  -th cell in the
-th cell in the  -th row and the
-th row and the 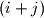 -th cell in the
-th cell in the  -th row have the same colour. (The indices of the cells in a row are considered modulo
-th row have the same colour. (The indices of the cells in a row are considered modulo 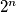 .) Prove that the maximal possible number of colours is
.) Prove that the maximal possible number of colours is 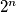 .
.Proposed by Hossein Dabirian, Sepehr Ghazi-nezami, Iran
Izvor: Međunarodna matematička olimpijada, shortlist 2010
 Školjka
Školjka 
