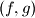
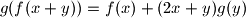
Determine all pairs of functions from the set of real numbers to itsels that satisfy for all real numbers and
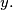
Proposed by Japan
%V0
Determine all pairs $(f,g)$ of functions from the set of real numbers to itsels that satisfy $$g(f(x+y)) = f(x) + (2x + y)g(y)$$ for all real numbers $x$ and $y.$
Proposed by Japan
Izvor: Međunarodna matematička olimpijada, shortlist 2011
Školjka 
of functions from the set of real numbers to itsels that satisfy 
for all real numbers 
and 