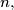
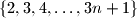
Prove that for every positive integer the set can be partitioned into triples in such a way that the numbers from each triple are the lengths of the sides of some obtuse triangle.
Proposed by Canada
%V0
Prove that for every positive integer $n,$ the set $\{2,3,4,\ldots,3n+1\}$ can be partitioned into $n$ triples in such a way that the numbers from each triple are the lengths of the sides of some obtuse triangle.
Proposed by Canada
Izvor: Međunarodna matematička olimpijada, shortlist 2011
Školjka 
the set 
can be partitioned into 
triples in such a way that the numbers from each triple are the lengths of the sides of some obtuse triangle.