IMO Shortlist 2011 problem A7
Dodao/la:
arhiva23. lipnja 2013. Let
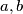
and

be positive real numbers satisfying
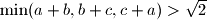
and
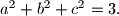
Prove that
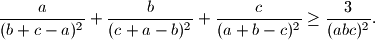
Proposed by Titu Andrescu, Saudi Arabia
%V0
Let $a,b$ and $c$ be positive real numbers satisfying $\min(a+b,b+c,c+a) > \sqrt{2}$ and $a^2+b^2+c^2=3.$ Prove that
$$\frac{a}{(b+c-a)^2} + \frac{b}{(c+a-b)^2} + \frac{c}{(a+b-c)^2} \geq \frac{3}{(abc)^2}.$$
Proposed by Titu Andrescu, Saudi Arabia
Izvor: Međunarodna matematička olimpijada, shortlist 2011