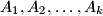
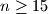
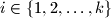
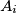
Determine the greatest positive integer that satisfies the following property: The set of positive integers can be partitioned into subsets such that for all integers and all there exist two distinct elements of whose sum is
Proposed by Igor Voronovich, Belarus
%V0
Determine the greatest positive integer $k$ that satisfies the following property: The set of positive integers can be partitioned into $k$ subsets $A_1, A_2, \ldots, A_k$ such that for all integers $n \geq 15$ and all $i \in \{1, 2, \ldots, k\}$ there exist two distinct elements of $A_i$ whose sum is $n.$
Proposed by Igor Voronovich, Belarus
Source: Međunarodna matematička olimpijada, shortlist 2011
Školjka 
that satisfies the following property: The set of positive integers can be partitioned into 
such that for all integers 
and all 
there exist two distinct elements of 
whose sum is 