IMO Shortlist 2011 problem C6
Kvaliteta:
Avg: 3,0Težina:
Avg: 8,0 Let  be a positive integer, and let
be a positive integer, and let 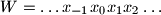 be an infinite periodic word, consisting of just letters
be an infinite periodic word, consisting of just letters  and/or
and/or  . Suppose that the minimal period
. Suppose that the minimal period  of
of  is greater than
is greater than 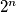 .
.
A finite nonempty word is said to appear in
is said to appear in  if there exist indices
if there exist indices 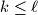 such that
such that 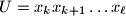 . A finite word
. A finite word  is called ubiquitous if the four words
is called ubiquitous if the four words 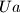 ,
, 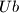 ,
, 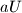 , and
, and 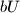 all appear in
all appear in  . Prove that there are at least
. Prove that there are at least  ubiquitous finite nonempty words.
ubiquitous finite nonempty words.
Proposed by Grigory Chelnokov, Russia
 be a positive integer, and let
be a positive integer, and let 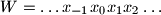 be an infinite periodic word, consisting of just letters
be an infinite periodic word, consisting of just letters  and/or
and/or  . Suppose that the minimal period
. Suppose that the minimal period  of
of  is greater than
is greater than 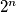 .
.A finite nonempty word
 is said to appear in
is said to appear in  if there exist indices
if there exist indices 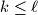 such that
such that 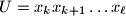 . A finite word
. A finite word  is called ubiquitous if the four words
is called ubiquitous if the four words 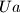 ,
, 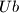 ,
, 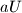 , and
, and 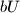 all appear in
all appear in  . Prove that there are at least
. Prove that there are at least  ubiquitous finite nonempty words.
ubiquitous finite nonempty words.Proposed by Grigory Chelnokov, Russia
Izvor: Međunarodna matematička olimpijada, shortlist 2011
 Školjka
Školjka 
