IMO Shortlist 2011 problem G2
Dodao/la:
arhiva23. lipnja 2013. Let
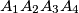
be a non-cyclic quadrilateral. Let
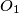
and
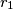
be the circumcentre and the circumradius of the triangle
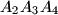
. Define
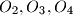
and
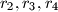
in a similar way. Prove that
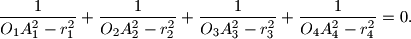
Proposed by Alexey Gladkich, Israel
%V0
Let $A_1A_2A_3A_4$ be a non-cyclic quadrilateral. Let $O_1$ and $r_1$ be the circumcentre and the circumradius of the triangle $A_2A_3A_4$. Define $O_2,O_3,O_4$ and $r_2,r_3,r_4$ in a similar way. Prove that
$$\frac{1}{O_1A_1^2-r_1^2}+\frac{1}{O_2A_2^2-r_2^2}+\frac{1}{O_3A_3^2-r_3^2}+\frac{1}{O_4A_4^2-r_4^2}=0.$$
Proposed by Alexey Gladkich, Israel
Izvor: Međunarodna matematička olimpijada, shortlist 2011