IMO Shortlist 2011 problem G3
Kvaliteta:
Avg: 3,0Težina:
Avg: 7,0 Let  be a convex quadrilateral whose sides
be a convex quadrilateral whose sides  and
and  are not parallel. Suppose that the circles with diameters
are not parallel. Suppose that the circles with diameters  and
and  meet at points
meet at points  and
and  inside the quadrilateral. Let
inside the quadrilateral. Let 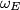 be the circle through the feet of the perpendiculars from
be the circle through the feet of the perpendiculars from  to the lines
to the lines 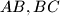 and
and  . Let
. Let 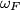 be the circle through the feet of the perpendiculars from
be the circle through the feet of the perpendiculars from  to the lines
to the lines 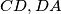 and
and  . Prove that the midpoint of the segment
. Prove that the midpoint of the segment  lies on the line through the two intersections of
lies on the line through the two intersections of 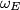 and
and 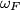 .
.
Proposed by Carlos Yuzo Shine, Brazil
 be a convex quadrilateral whose sides
be a convex quadrilateral whose sides  and
and  are not parallel. Suppose that the circles with diameters
are not parallel. Suppose that the circles with diameters  and
and  meet at points
meet at points  and
and  inside the quadrilateral. Let
inside the quadrilateral. Let 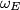 be the circle through the feet of the perpendiculars from
be the circle through the feet of the perpendiculars from  to the lines
to the lines 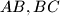 and
and  . Let
. Let 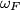 be the circle through the feet of the perpendiculars from
be the circle through the feet of the perpendiculars from  to the lines
to the lines 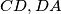 and
and  . Prove that the midpoint of the segment
. Prove that the midpoint of the segment  lies on the line through the two intersections of
lies on the line through the two intersections of 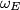 and
and 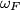 .
.Proposed by Carlos Yuzo Shine, Brazil
Izvor: Međunarodna matematička olimpijada, shortlist 2011
 Školjka
Školjka 
