IMO Shortlist 2011 problem G4
Kvaliteta:
Avg: 0,0Težina:
Avg: 7,0 Let  be an acute triangle with circumcircle
be an acute triangle with circumcircle 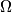 . Let
. Let 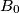 be the midpoint of
be the midpoint of  and let
and let 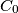 be the midpoint of
be the midpoint of  . Let
. Let  be the foot of the altitude from
be the foot of the altitude from  and let
and let 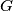 be the centroid of the triangle
be the centroid of the triangle  . Let
. Let 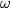 be a circle through
be a circle through 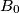 and
and 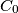 that is tangent to the circle
that is tangent to the circle 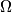 at a point
at a point 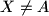 . Prove that the points
. Prove that the points 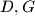 and
and  are collinear.
are collinear.
Proposed by Ismail Isaev and Mikhail Isaev, Russia
 be an acute triangle with circumcircle
be an acute triangle with circumcircle 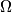 . Let
. Let 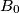 be the midpoint of
be the midpoint of  and let
and let 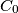 be the midpoint of
be the midpoint of  . Let
. Let  be the foot of the altitude from
be the foot of the altitude from  and let
and let 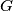 be the centroid of the triangle
be the centroid of the triangle  . Let
. Let 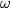 be a circle through
be a circle through 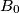 and
and 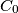 that is tangent to the circle
that is tangent to the circle 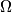 at a point
at a point 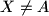 . Prove that the points
. Prove that the points 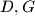 and
and  are collinear.
are collinear.Proposed by Ismail Isaev and Mikhail Isaev, Russia
Izvor: Međunarodna matematička olimpijada, shortlist 2011
Komentari:
fini_keksi, 25. siječnja 2023. 10:51
 Školjka
Školjka 
