IMO Shortlist 2011 problem G5
Kvaliteta:
Avg: 0,0Težina:
Avg: 8,0 Let  be a triangle with incentre
be a triangle with incentre  and circumcircle
and circumcircle  . Let
. Let  and
and  be the second intersection points of
be the second intersection points of  with
with 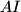 and
and 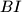 , respectively. The chord
, respectively. The chord 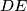 meets
meets  at a point
at a point  , and
, and  at a point
at a point  . Let
. Let  be the intersection point of the line through
be the intersection point of the line through  parallel to
parallel to  and the line through
and the line through  parallel to
parallel to  . Suppose that the tangents to
. Suppose that the tangents to  at
at  and
and  meet at a point
meet at a point  . Prove that the three lines
. Prove that the three lines 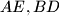 and
and 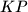 are either parallel or concurrent.
are either parallel or concurrent.
Proposed by Irena Majcen and Kris Stopar, Slovenia
 be a triangle with incentre
be a triangle with incentre  and circumcircle
and circumcircle  . Let
. Let  and
and  be the second intersection points of
be the second intersection points of  with
with 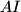 and
and 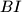 , respectively. The chord
, respectively. The chord 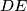 meets
meets  at a point
at a point  , and
, and  at a point
at a point  . Let
. Let  be the intersection point of the line through
be the intersection point of the line through  parallel to
parallel to  and the line through
and the line through  parallel to
parallel to  . Suppose that the tangents to
. Suppose that the tangents to  at
at  and
and  meet at a point
meet at a point  . Prove that the three lines
. Prove that the three lines 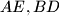 and
and 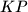 are either parallel or concurrent.
are either parallel or concurrent.Proposed by Irena Majcen and Kris Stopar, Slovenia
Izvor: Međunarodna matematička olimpijada, shortlist 2011
 Školjka
Školjka 
