IMO Shortlist 2011 problem N1
Dodao/la:
arhiva23. lipnja 2013. For any integer
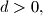
let
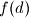
be the smallest possible integer that has exactly

positive divisors (so for example we have
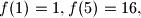
and
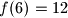
). Prove that for every integer
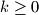
the number
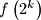
divides
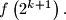
Proposed by Suhaimi Ramly, Malaysia
%V0
For any integer $d > 0,$ let $f(d)$ be the smallest possible integer that has exactly $d$ positive divisors (so for example we have $f(1)=1, f(5)=16,$ and $f(6)=12$). Prove that for every integer $k \geq 0$ the number $f\left(2^k\right)$ divides $f\left(2^{k+1}\right).$
Proposed by Suhaimi Ramly, Malaysia
Izvor: Međunarodna matematička olimpijada, shortlist 2011