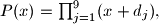
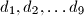
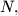
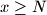
Consider a polynomial where are nine distinct integers. Prove that there exists an integer such that for all integers the number is divisible by a prime number greater than 20.
Proposed by Luxembourg
%V0
Consider a polynomial $P(x) = \prod^9_{j=1}(x+d_j),$ where $d_1, d_2, \ldots d_9$ are nine distinct integers. Prove that there exists an integer $N,$ such that for all integers $x \geq N$ the number $P(x)$ is divisible by a prime number greater than 20.
Proposed by Luxembourg
Izvor: Međunarodna matematička olimpijada, shortlist 2011
Školjka 
where 
are nine distinct integers. Prove that there exists an integer 
such that for all integers 
the number 
is divisible by a prime number greater than 20.