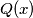
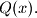
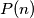
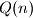
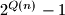
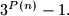
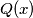
Let and be two polynomials with integer coefficients, such that no nonconstant polynomial with rational coefficients divides both and Suppose that for every positive integer the integers and are positive, and divides Prove that is a constant polynomial.
Proposed by Oleksiy Klurman, Ukraine
%V0
Let $P(x)$ and $Q(x)$ be two polynomials with integer coefficients, such that no nonconstant polynomial with rational coefficients divides both $P(x)$ and $Q(x).$ Suppose that for every positive integer $n$ the integers $P(n)$ and $Q(n)$ are positive, and $2^{Q(n)}-1$ divides $3^{P(n)}-1.$ Prove that $Q(x)$ is a constant polynomial.
Proposed by Oleksiy Klurman, Ukraine
Izvor: Međunarodna matematička olimpijada, shortlist 2011
Školjka 
and 
be two polynomials with integer coefficients, such that no nonconstant polynomial with rational coefficients divides both 
Suppose that for every positive integer 
the integers 
and 
are positive, and 
divides 
Prove that