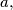
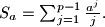
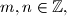
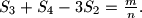
Let be an odd prime number. For every integer define the number Let such that Prove that divides
Proposed by Romeo Meštrović, Montenegro
%V0
Let $p$ be an odd prime number. For every integer $a,$ define the number $S_a = \sum^{p-1}_{j=1} \frac{a^j}{j}.$ Let $m,n \in \mathbb{Z},$ such that $S_3 + S_4 - 3S_2 = \frac{m}{n}.$ Prove that $p$ divides $m.$
Proposed by Romeo Meštrović, Montenegro
Izvor: Međunarodna matematička olimpijada, shortlist 2011
Školjka 
be an odd prime number. For every integer 
define the number 
Let 
such that 
Prove that 