IMO Shortlist 2011 problem N8
Dodao/la:
arhiva23. lipnja 2013. Let
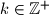
and set
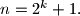
Prove that

is a prime number if and only if the following holds: there is a permutation
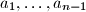
of the numbers
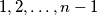
and a sequence of integers
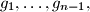
such that

divides
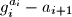
for every

where we set
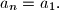
Proposed by Vasily Astakhov, Russia
%V0
Let $k \in \mathbb{Z}^+$ and set $n=2^k+1.$ Prove that $n$ is a prime number if and only if the following holds: there is a permutation $a_{1},\ldots,a_{n-1}$ of the numbers $1,2, \ldots, n-1$ and a sequence of integers $g_{1},\ldots,g_{n-1},$ such that $n$ divides $g^{a_i}_i - a_{i+1}$ for every $i \in \{1,2,\ldots,n-1\},$ where we set $a_n = a_1.$
Proposed by Vasily Astakhov, Russia
Izvor: Međunarodna matematička olimpijada, shortlist 2011