IMO Shortlist 2012 problem A7
Dodao/la:
arhiva3. studenoga 2013. We say that a function
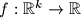
is a metapolynomial if, for some positive integer

and

, it can be represented in the form
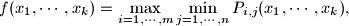
where
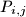
are multivariate polynomials. Prove that the product of two metapolynomials is also a metapolynomial.
%V0
We say that a function $f:\mathbb{R}^k \rightarrow \mathbb{R}$ is a metapolynomial if, for some positive integer $m$ and $n$, it can be represented in the form
$$f(x_1,\cdots , x_k )=\max_{i=1,\cdots , m} \min_{j=1,\cdots , n}P_{i,j}(x_1,\cdots , x_k),$$
where $P_{i,j}$ are multivariate polynomials. Prove that the product of two metapolynomials is also a metapolynomial.
Izvor: Međunarodna matematička olimpijada, shortlist 2012