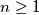
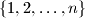
Let be an integer. What is the maximum number of disjoint pairs of elements of the set such that the sums of the different pairs are different integers not exceeding ?
%V0
Let $n \geq 1$ be an integer. What is the maximum number of disjoint pairs of elements of the set $\{ 1,2,\ldots , n \}$ such that the sums of the different pairs are different integers not exceeding $n$?
Izvor: Međunarodna matematička olimpijada, shortlist 2012
Školjka 
be an integer. What is the maximum number of disjoint pairs of elements of the set 
such that the sums of the different pairs are different integers not exceeding 
?