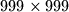
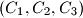
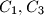
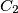
In a square table some cells are white and the remaining ones are red. Let be the number of triples of cells, the first two in the same row and the last two in the same column, with white and red. Find the maximum value can attain.
%V0
In a $999 \times 999$ square table some cells are white and the remaining ones are red. Let $T$ be the number of triples $(C_1,C_2,C_3)$ of cells, the first two in the same row and the last two in the same column, with $C_1,C_3$ white and $C_2$ red. Find the maximum value $T$ can attain.
Izvor: Međunarodna matematička olimpijada, shortlist 2012
Školjka 
square table some cells are white and the remaining ones are red. Let 
be the number of triples 
of cells, the first two in the same row and the last two in the same column, with 
white and 
red. Find the maximum value