IMO Shortlist 2012 problem C5
Kvaliteta:
Avg: 0,0Težina:
Avg: 8,0 The columns and the row of a 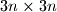 square board are numbered
square board are numbered 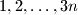 . Every square
. Every square 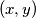 with
with 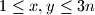 is colored asparagus, byzantium or citrine according as the modulo
is colored asparagus, byzantium or citrine according as the modulo  remainder of
remainder of 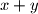 is
is 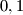 or
or  respectively. One token colored asparagus, byzantium or citrine is placed on each square, so that there are
respectively. One token colored asparagus, byzantium or citrine is placed on each square, so that there are 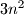 tokens of each color.
tokens of each color.
Suppose that on can permute the tokens so that each token is moved to a distance of at most from its original position, each asparagus token replaces a byzantium token, each byzantium token replaces a citirine token, and each citrine token replaces an aspargus token. Prove that it is possible to permute the tokens so that each token is moved to a distance of at most
from its original position, each asparagus token replaces a byzantium token, each byzantium token replaces a citirine token, and each citrine token replaces an aspargus token. Prove that it is possible to permute the tokens so that each token is moved to a distance of at most 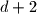 from its original position, and each square contains a token with the same color as the square.
from its original position, and each square contains a token with the same color as the square.
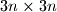 square board are numbered
square board are numbered 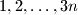 . Every square
. Every square 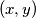 with
with 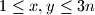 is colored asparagus, byzantium or citrine according as the modulo
is colored asparagus, byzantium or citrine according as the modulo  remainder of
remainder of 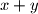 is
is 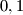 or
or  respectively. One token colored asparagus, byzantium or citrine is placed on each square, so that there are
respectively. One token colored asparagus, byzantium or citrine is placed on each square, so that there are 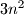 tokens of each color.
tokens of each color.Suppose that on can permute the tokens so that each token is moved to a distance of at most
 from its original position, each asparagus token replaces a byzantium token, each byzantium token replaces a citirine token, and each citrine token replaces an aspargus token. Prove that it is possible to permute the tokens so that each token is moved to a distance of at most
from its original position, each asparagus token replaces a byzantium token, each byzantium token replaces a citirine token, and each citrine token replaces an aspargus token. Prove that it is possible to permute the tokens so that each token is moved to a distance of at most 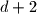 from its original position, and each square contains a token with the same color as the square.
from its original position, and each square contains a token with the same color as the square. Izvor: Međunarodna matematička olimpijada, shortlist 2012
 Školjka
Školjka 
