IMO Shortlist 2012 problem C7
Dodao/la:
arhiva3. studenoga 2013. There are given
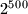
points on a circle labeled
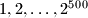
in some order. Prove that one can choose
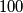
pairwise disjoint chords joining some of theses points so that the
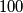
sums of the pairs of numbers at the endpoints of the chosen chord are equal.
%V0
There are given $2^{500}$ points on a circle labeled $1,2,\ldots ,2^{500}$ in some order. Prove that one can choose $100$ pairwise disjoint chords joining some of theses points so that the $100$ sums of the pairs of numbers at the endpoints of the chosen chord are equal.
Izvor: Međunarodna matematička olimpijada, shortlist 2012