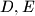
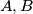
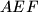
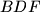
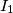
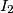
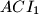
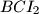
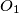
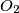
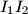
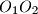
In an acute triangle the points and are the feet of the altitudes through and respectively. The incenters of the triangles and are and respectively; the circumcenters of the triangles and are and respectively. Prove that and are parallel.
%V0
In an acute triangle $ABC$ the points $D,E$ and $F$ are the feet of the altitudes through $A,B$ and $C$ respectively. The incenters of the triangles $AEF$ and $BDF$ are $I_1$ and $I_2$ respectively; the circumcenters of the triangles $ACI_1$ and $BCI_2$ are $O_1$ and $O_2$ respectively. Prove that $I_1I_2$ and $O_1O_2$ are parallel.
Izvor: Međunarodna matematička olimpijada, shortlist 2012
Školjka 
the points 
and 
are the feet of the altitudes through 
and 
respectively. The incenters of the triangles 
and 
are 
and 
respectively; the circumcenters of the triangles 
and 
are 
and 
respectively. Prove that 
and 
are parallel.