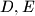
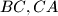
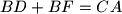
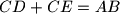
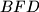
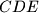
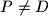
Let be a triangle with circumcenter and incenter . The points and on the sides and respectively are such that and . The circumcircles of the triangles and intersect at . Prove that .
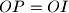
%V0
Let $ABC$ be a triangle with circumcenter $O$ and incenter $I$. The points $D,E$ and $F$ on the sides $BC,CA$ and $AB$ respectively are such that $BD+BF=CA$ and $CD+CE=AB$. The circumcircles of the triangles $BFD$ and $CDE$ intersect at $P \neq D$. Prove that $OP=OI$.
Izvor: Međunarodna matematička olimpijada, shortlist 2012
Školjka 
be a triangle with circumcenter 
and incenter 
. The points 
and 
on the sides 
and 
respectively are such that 
and 
. The circumcircles of the triangles 
and 
intersect at 
. Prove that 
.