IMO Shortlist 2012 problem N1
Dodao/la:
arhiva3. studenoga 2013. Call admissible a set

of integers that has the following property:
If
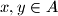
(possibly
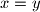
) then
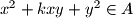
for every integer

.
Determine all pairs
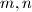
of nonzero integers such that the only admissible set containing both

and

is the set of all integers.
Proposed by Warut Suksompong, Thailand
%V0
Call admissible a set $A$ of integers that has the following property:
If $x,y \in A$ (possibly $x=y$) then $x^2+kxy+y^2 \in A$ for every integer $k$.
Determine all pairs $m,n$ of nonzero integers such that the only admissible set containing both $m$ and $n$ is the set of all integers.
Proposed by Warut Suksompong, Thailand
Izvor: Međunarodna matematička olimpijada, shortlist 2012