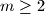
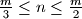
Determine all integers such that every with divides the binomial coefficient .
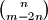
%V0
Determine all integers $m \geq 2$ such that every $n$ with $\frac{m}{3} \leq n \leq \frac{m}{2}$ divides the binomial coefficient $\binom{n}{m-2n}$.
Izvor: Međunarodna matematička olimpijada, shortlist 2012
Školjka 
such that every 
with 
divides the binomial coefficient 
.