IMO Shortlist 2012 problem N4
Dodao/la:
arhiva3. studenoga 2013. An integer

is called friendly if the equation
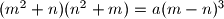
has a solution over the positive integers.
a) Prove that there are at least
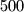
friendly integers in the set
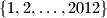
.
b) Decide whether
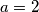
is friendly.
%V0
An integer $a$ is called friendly if the equation $(m^2+n)(n^2+m)=a(m-n)^3$ has a solution over the positive integers.
a) Prove that there are at least $500$ friendly integers in the set $\{ 1,2,\ldots ,2012\}$.
b) Decide whether $a=2$ is friendly.
Izvor: Međunarodna matematička olimpijada, shortlist 2012