IMO Shortlist 2012 problem N6
Dodao/la:
arhiva3. studenoga 2013. Let

and

be positive integers. If
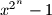
is divisible by
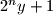
for every positive integer

, prove that
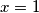
.
%V0
Let $x$ and $y$ be positive integers. If $x^{2^n}-1$ is divisible by $2^ny+1$ for every positive integer $n$, prove that $x=1$.
Izvor: Međunarodna matematička olimpijada, shortlist 2012