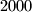
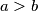
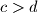
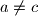
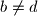
Prove that in any set of distinct real numbers there exist two pairs and with or such that
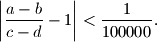
%V0
Prove that in any set of $2000$ distinct real numbers there exist two pairs $a > b$ and $c > d$ with $a \neq c$ or $b \neq d$ such that $$
\left| \frac{a-b}{c-d} - 1 \right| < \frac{1}{100000} \text{.}
$$
Školjka 
distinct real numbers there exist two pairs 
and 
with 
or 
such that 