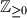
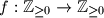
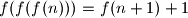
Let be the set of all nonnegative integers. Find all the functions satisfying the relation for all .
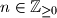
%V0
Let $\mathbb{Z}_{\geq0}$ be the set of all nonnegative integers. Find all the functions $f : \mathbb{Z}_{\geq0} \to \mathbb{Z}_{\geq0}$ satisfying the relation $$
f(f(f(n))) = f(n + 1) + 1
$$ for all $n \in \mathbb{Z}_{\geq0}$.
Školjka 
be the set of all nonnegative integers. Find all the functions 
satisfying the relation 
for all 
.