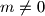
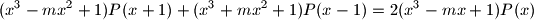
Let be an integer. Find all polynomials with real coefficients such that for all real numbers .
%V0
Let $m \neq 0$ be an integer. Find all polynomials $P(x)$ with real coefficients such that $$
(x^3 - m x^2 + 1)P(x + 1) + (x^3 + m x^2 + 1)P(x - 1) = 2(x^3 - m x + 1)P(x)
$$ for all real numbers $x$.
Školjka 
be an integer. Find all polynomials 
with real coefficients such that 
for all real numbers 
.