Let

be a positive integer, and let
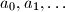
be an infinite sequence of real numbers. Assume that for all nonnegative integers

and

there exists a positive integer
![n \in [m + 1, m + r]](/media/m/5/d/7/5d7b59438e77c03c392bfe9a83659e20.png)
such that
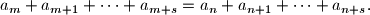
Prove that the sequence is periodic, i.e. there exists some
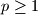
such that
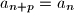
for all
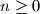
.
%V0
Let $r$ be a positive integer, and let $a_0, a_1, \ldots$ be an infinite sequence of real numbers. Assume that for all nonnegative integers $m$ and $s$ there exists a positive integer $n \in [m + 1, m + r]$ such that $$
a_m + a_{m+1} + \cdots + a_{m+s} = a_n + a_{n+1} + \cdots + a_{n+s} \text{.}
$$
Prove that the sequence is periodic, i.e. there exists some $p \geq 1$ such that $a_{n+p} = a_n$ for all $n \geq 0$.