IMO Shortlist 2013 problem C8
Kvaliteta:
Avg: 0,0Težina:
Avg: 9,0 Players  and
and  play a paintful game on the real line. Player
play a paintful game on the real line. Player  has a pot of paint with four units of black ink. A quantity
has a pot of paint with four units of black ink. A quantity  of this ink suffices to blacken a (closed) real interval of length
of this ink suffices to blacken a (closed) real interval of length  . In every round, player
. In every round, player  picks some positive integer
picks some positive integer  and provides
and provides 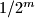 units of ink from the pot. Player
units of ink from the pot. Player  then picks an integer
then picks an integer  and blackens the interval from
and blackens the interval from 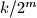 to
to 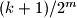 (some parts of this interval may have been blackened before). The goal of player
(some parts of this interval may have been blackened before). The goal of player  is to reach a situation where the pot is empty and the interval
is to reach a situation where the pot is empty and the interval ![[0, 1]](/media/m/7/f/0/7f04c41d91b0555ac792351e836cbd4e.png) is not completely blackened.
is not completely blackened.
Decide whether there exists a strategy for player to win in a finite number of moves.
to win in a finite number of moves.
 and
and  play a paintful game on the real line. Player
play a paintful game on the real line. Player  has a pot of paint with four units of black ink. A quantity
has a pot of paint with four units of black ink. A quantity  of this ink suffices to blacken a (closed) real interval of length
of this ink suffices to blacken a (closed) real interval of length  . In every round, player
. In every round, player  picks some positive integer
picks some positive integer  and provides
and provides 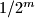 units of ink from the pot. Player
units of ink from the pot. Player  then picks an integer
then picks an integer  and blackens the interval from
and blackens the interval from 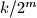 to
to 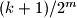 (some parts of this interval may have been blackened before). The goal of player
(some parts of this interval may have been blackened before). The goal of player  is to reach a situation where the pot is empty and the interval
is to reach a situation where the pot is empty and the interval ![[0, 1]](/media/m/7/f/0/7f04c41d91b0555ac792351e836cbd4e.png) is not completely blackened.
is not completely blackened.Decide whether there exists a strategy for player
 to win in a finite number of moves.
to win in a finite number of moves. Izvor: Austria
 Školjka
Školjka 
